20 Monitoring Approximate Convergence
We know that if we run an ergodic Markov chain long enough, it will eventually approach stationarity. We can even use the entire chain for estimation if we run long enough because eny finite error will become infinitesimal in the asymptotic regime.
However, we do not live in the asymptotic regime. We need results that we can trust from finitely many draws. If we happened to know our chains were geometrically ergodic, so that we know they converged very quickly toward the stationry distribution, then our lives would be easy and we cold proceed with a single chain and as long as there weren’t numerical problems, we could run it a long time and trust it.
We are also faced with distributions defined implicitly as posteriors, whose geometric ergodicity is difficult, if not impossible, to establish theoretically. Therefore, we need finite-sample diagnostics in order to test whether our chains have reached a stationary distribution which we can trust for estimation.
20.1 Running multiple chains
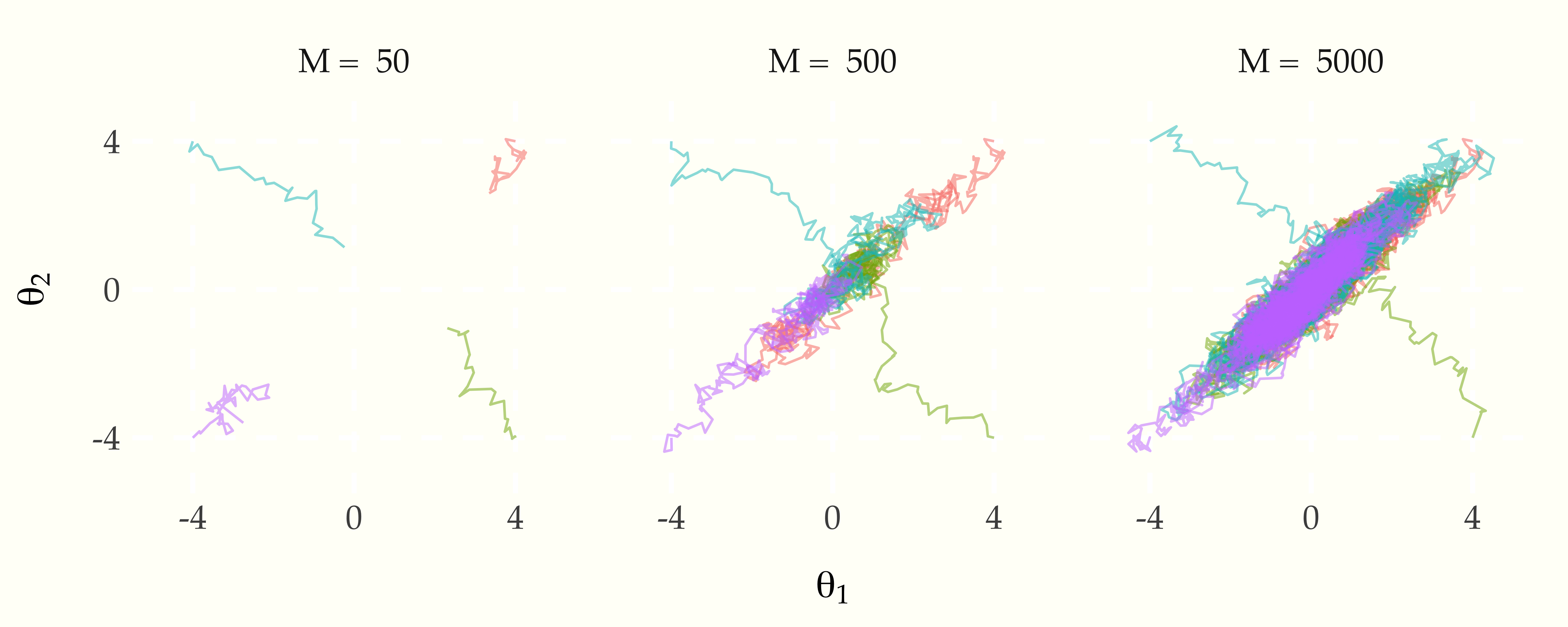
One way to diagnose non-convergence is to run multiple chains and monitor various statistics, which should match among the different chains. As an example, consider the two-dimensional Metropolis example. Starting four chains in the corners and running for various number of time steps shows how the chains approach stationarity.
Figure 20.1: The evolution of four random walk Metropolis Markov chains, each started in a different corner of the plot. The target density is bivariate normal with correlation 0.9 and unit variance; the random walk step size is 0.2. After \(M = 50\) iterations, the chains have not arrived at the typical set. After \(M = 500\) iterations, the chains have each arrived in the typical set, but they have not had time to mix. After \(M = 5000\) iterations, the chains are mixing well and have visited most of the target density.